Other than being able to find your birthday in Pi, why is Pi important enough to deserve a day of its own -- and a search engine to draw attention to it? Well, let's start with the basics...

Pi (π) is the ratio of the circumference of a circle to its diameter. It doesn't matter how big or small the circle is - the ratio stays the same. Properties like this that stay the same when you change other attributes are called constants. Because it's so easily observed (you can measure it with a piece of string!), Pi has been popular for centuries.
Pi is easy to observe, but hard to compute accurately by hand.
- You can measure Pi by constructing a physical wheel and rolling it out - but you won't get more than a digit or two of accuracy.
- You can measure Pi by bracketing a circle with polygons. This is easy with polygons with small numbers of sides, but it gets harder as you add sides. Archimedes used this trick with 96 sided polygons to correctly estimate Pi to about two digits (3.14), proving 3.1408 < Pi < 3.1428. You can try this trick with squares:
The outer square has a side length of 1 (the same as the circle's diameter). The square we stuffed inside the circle has a diagonal length of 1. Importantly, it's a right triangle (the corner angle is 90 degrees), so we can usee the Pythagorean theorem a2 + b2 = c2 to determine the length of the sides: c2 = 1, and a and b have the same length, so 2 * side2 = 1. The length of the side, then, is √1/2.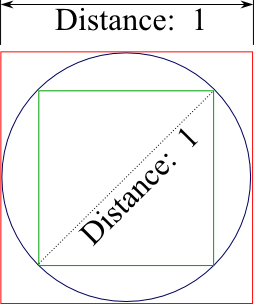
From the side lengths, we can compute the circumference of the two squares. The outer square obviously has a circumference of 4, and the inner square has a circumference of 4 * √1/2, which is roughly 2.828. So we've proved some very loose bounds on Pi - and now you can see why Archimedes had to go up to a 96-sided polygon before he started getting good results!
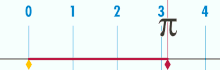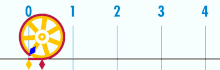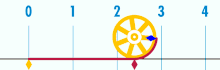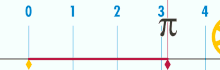 |
| Take a circle whose diameter (all the way across) is 1. If you roll it until you get back to the start, it will measure out Pi units. (Image from Wikipedia) |
Methods to estimate Pi demonstrate several significant advances in mathematics
These days, we have better tricks for estimating Pi than the circumscribed-circle method used by Archimedes, but progress was mind-numbingly slow - and came due to advances in calculus and computing infinite series. See the Wikipedia Chronology of Computation of Pi for more cool detail.
| Year | Digits | Value |
|---|---|---|
| 26th century BC - Ancient Egypt | 3 | 22/7 = 3.14... |
| 250 BC - Archimedes | 3 | 3.1408 < Pi < 3.1428 |
| 150 AD - Ptolemy | 4 | 3.141666... |
| 480 AD - Zu Chongzhi | 6 | 3.1415926 < Pi < 3.1415927 |
| 1400 - Madhava of Sangamagrama | 11 | |
| 1424 Jamshid al-Kashi | 16 | |
| 1621 Ludolph van Ceulen + student | 35 | |
| 1699 | 71 | |
| 1706 | 100 | |
| 1794 | 137 | |
| 1841 | 152 | |
| 1844 | 200 | |
| 1853 | 440 | |
| 1874 - last before calculators | 527 |
And computing Pi demonstrated advances in computing...
After the invention of the calculator and then computer, the records jumped drastically. In 1949, Ferguson and Wrench computed 1,120 digits using a desk calculator. The first computer attempt, in 1949 on the ENIAC (the first general-purpose electronic computer), took 70 hours and computed 2037 decimal places. By 1967, the record stood at half a million digits, and in 2009, Takahashi et al. used a supercomputer to compute 2.5 trillion digits of Pi. But it didn't stop there...
The first computational results used massive computers. But on the last day of 2009, Fabrice Bellard used a home computer - running an Intel Core i7 CPU similar to what you might be using today in 2011 to read this website - to compute 2.7 trillion places. And the most recent record of 10 trillion digits of Pi was computed by Alexander J. Yee and Shigeru Kondo in 2011 using a fast, but not crazy, dual processor Intel Xeon-bsed machine with a huge amount of hard disk space.
Today, you can even compute thounsands of digits of Pi on your iPhone, something that might just have blown the mind of mathematicians 2000 years ago.
Click here to see our set of some programs to play with Pi on your own
